数组,树和哈希表
现在我们已经明白了时间复杂度和排序的思想,接下来我要告诉你三个数据结构。这些数据结构都很重要,因为它们是现代数据库的骨架。我也会引入数据库索引这一概念。
数组
二维数组是最简单的数据结构。表格可以被当成是一个数组。例如:
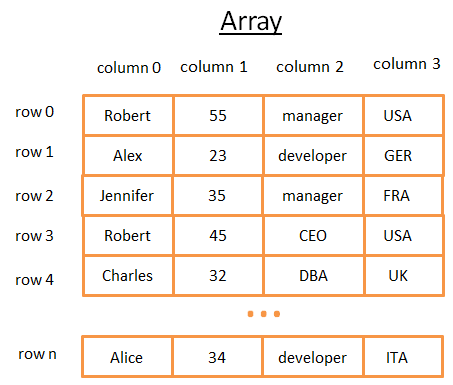
这个二维数组就是带有行和列的表格:
- 每一行表示一个对象
- 每一列描述对象的特征
- 每一列存储一种特定的数据类型(整型,字符串,日期等)
虽然这种数据结构非常适合与保存和数据可视化,但是当你需要查找一个特定值时,这种结构就玩不转了。
例如,如果你想找到所有在英国工作的人,你需要遍历每一行,去看看这一行是不是属于英国。这需要消耗 N 个操作(N 是行数),这看起来还不算很坏,但是有更快的吗?这就是引入树的目的。
注意,大多数现代数据库提供了改进数组,用于有效存储表,例如堆组织表(heap-organized tables)和索引组织表(index-organized tables)。但是,这些并不能改变快速检索符合特定条件的列组的问题。
树和数据库索引
二叉搜索树是带有特殊属性的二叉树,其每个节点的键必须满足:
- 大于所有左侧子树的键
- 小于所有右侧子树的键
下面我们来看看这是什么意思。
思想

这棵树有 N=15 个元素。假如说我要查找 208:
- 我从根节点开始找起,根节点的键是 136。由于 136<208,那么,我需要查找节点 136 的右侧子树
- 398>208,那么,我需要查找节点 398 的左侧子树
- 250>208,那么,我需要查找节点 250 的左侧子树
- 200<208,那么,我需要查找节点 200 的右侧子树。但是 200 没有右侧子树,因此,该值不存在(因为如果它存在,它应该在 200 的右侧子树)
现在,我要找 40:
- 我从根节点开始找起,根节点的键是 136。由于 136>40,那么,我需要查找节点 136 的左侧子树
- 80>40,那么,我需要查找节点 80 的左侧子树
- 40= 40,节点存在。我取出该节点中保存的行号(这一属性没有在上图展示出来),找到了给定行号的表
- 知道了行号,也就知道了数据在表中的确切位置,因此我就能直接取出。
最后,这两个检索都只耗费了树的层数那么多的操作。如果你认真阅读了合并排序的部分,你应该发现这棵树其实是有 log(N) 层。所以,检索消耗是 log(N),还不错!
回到问题
这些解释都有点抽象,让我们回到我们的问题。忘记前面愚蠢的整数吧,我们想想前面的表格中那些代表某人所在国家的字符串。加入你有一棵包含了表格中“国家”一列的树:
- 假设你想知道谁在英国工作
- 查找树,获得表示英国的节点
- 在那些“英国节点”中,你可以找到这些在英国工作的人所在行的位置
这个检索只会消耗 log(N) 个操作,而直接使用数组则需要 N 个操作。这个你想象中的东西就是数据库索引(database index)。
你可以为列的任意组合构造树索引(字符串、整型、2 个字符串、一个整型和一个字符串、日期等等),只要你能够有一个可以比较键值(也就是这些列的组合)的函数。该函数可以用来计算这些键值的顺序(数据库中的基本类型就是这种情况)。
B+ 树索引
虽然二叉搜索树适合于查找特定值,但是当你需要获取两个值之间的多个元素时,会有一个很大的问题。因为你必须检查树中的所有节点,看它是不是落在两个值之间(例如,使用树的中序遍历),二叉搜索树的消耗会达到 O(N)。更要命的是,由于你必须读取整棵树,因此这一操作不是磁盘 I/O 友好的。我们需要找到一个执行范围查询的有效方法。为解决这一问题,现代数据库使用了一种改进了的二叉搜索树,被称为 B+ 树。在 B+ 树中:
- 只有最低的节点(叶子节点)保存信息(相关表中的行的位置)
- 其它节点仅仅用来在检索中路由到正确的节点。
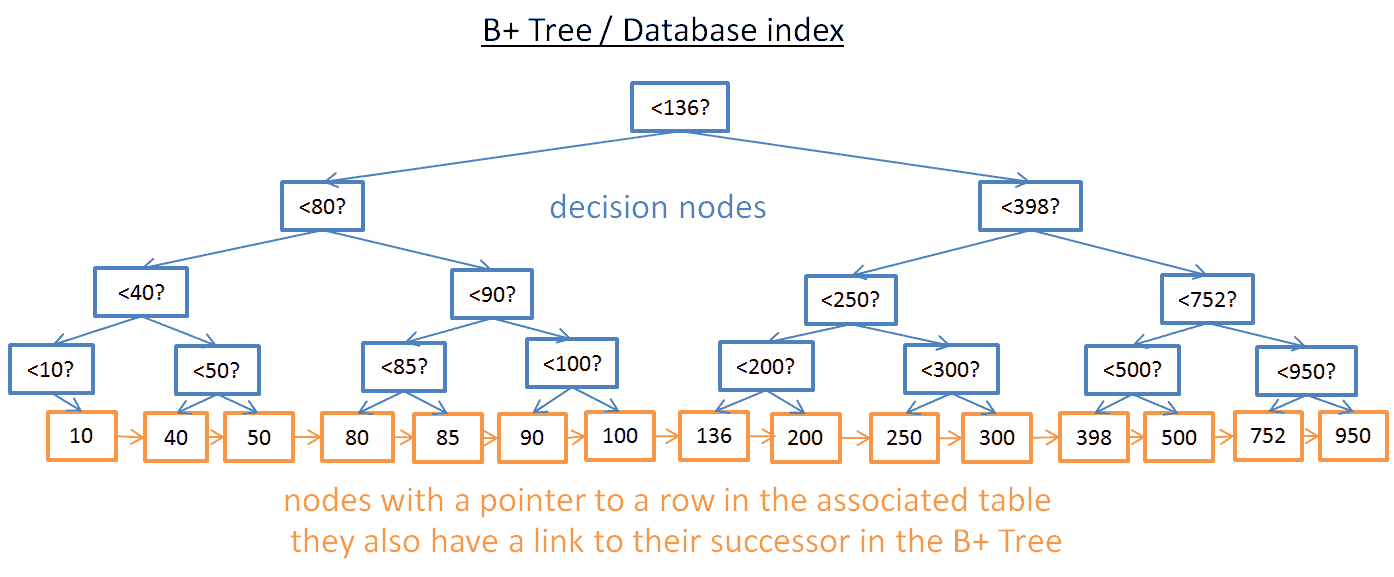
正如上图所示,B+ 树的节点更多(比二叉搜索树多出一倍)。事实上,你有一些额外的节点,这些“决策节点”会帮助你找到正确的节点(也就是保存相关表格行的位置的节点)。然而检索复杂度依然是 O(log(N))(仅仅多了一层)。最大的区别是,最低层节点与它们的后继节点连接起来。
使用 B+ 树,假设你正在查找 40 和 100 之间的值:
- 你需要像前面的树那样找到 40(如果 40 不存在的话,就选择大于 40 的最小值)
- 然后通过 40 的后继节点找到 100
假如你找到了 M 个后继节点,而树有 N 个节点。检索特定值就像前面的二叉搜索树一样耗费 log(N);一旦你找到了这个节点,通过它们的后继节点,你会在 M 个操作中找到 M 个后继。该检索仅消耗 M + log(N) 个操作,而前面的二叉搜索树则需要 N 个操作。另外,你不需要一次读取整棵树(只需要 M + log(N) 个节点),这意味着更少的磁盘使用。如果 M 很小(比如 200 行)而 N 很大(1 000 000 行),那就会有很大不同了。
但是,还有一些新的问题(又来!)。如果你向数据库新增或删除一行(因此也必须修改关联的 B+ 树索引):
- 你必须保持 B+ 树中的节点顺序,否则以后就不能在树中查找节点了
- 你必须尽可能减少 B+ 树的层数,否则时间复杂度就会从 O(log(N)) 变成 O(N)
换句话说,B+ 树必须是自排序的,并且是自平衡的。幸运的是,还真的有智能删除、插入操作。但是这也会导致一个消耗:B+ 树的插入和删除操作都是 O(log(N)) 的。这就是为什么你经常听到这样的话:过多地使用索引不是一个好主意。事实上,由于数据库需要更新表索引,而每一个索引的修改都是 O(log(N)) 的,因此,你正在拖慢原本很快的行插入、更新和删除操作。另外,添加索引意味着会给事务管理器带来更多工作负荷(我们会在文章的最后认识这个管理器)。
更多细节可以阅读百科有关 B+ 树的文章。如果你想要一个数据库中 B+ 树实现的例子,可以阅读 MySQL 的一位核心开发者的这篇文章和这篇文章。这两篇文章都关注于 innoDB(MySQL 的引擎之一)的索引处理。
注意:有位读者曾告诉我,考虑到数据库需要进行低层优化,B+ 树必须是完全平衡的。
哈希表
我们最后一个重要的数据结构是哈希表。当你需要快速查找值是,哈希表是非常有帮助的。另外,了解哈希表可以帮助我们理解一个通用的数据库连接操作,被称为哈希连接(hash join)。这种数据结构还被用于存储一些内部信息(比如锁表或缓冲池,我们会在后面见到这些概念)。
哈希表是一种使用键快速查找元素的数据结构。构建哈希表需要定义:
- 元素的键。
- 键的哈希函数。键通过哈希函数计算出来的哈希值给出了元素位置(称为桶)。
- 用于比较键的函数。一旦找到正确的桶,你需要使用这个比较函数在这个桶中找到你要查找的元素。
一个简单的例子
我们看一个可视化的例子:
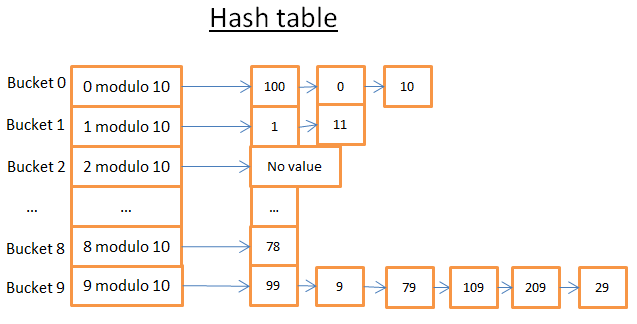


3 评论
有一点疑问:
在对比二叉树和B+树的时候
假设树的节点是N,想在里面寻找一个范围的节点,节点有M个
B+的算法是:先找到这个范围的起始点,然后通过对比取出M个节点,所以是O(M+log(N))
二叉树:得一个一个的去找这个范围的所有节点,例如从0到10,我就得先去二叉树中找出是否存在0,存在的话取出来,然后再找1......最后找10,由于找一个数的时间复杂度是O(log(N)),所以整个所需时间是O(M*log(N)),而不是上文提到的N,因为不需要把所有的值都找出来,只需要找这个范围里的值
不知道我的分析有没有道理
再次感谢您的分享
按照我的理解,当你检索一个区间 [a, b] 的时候,你并不知道 a 是不是存在于二叉搜索树中,也不知道树中究竟有几个元素落在 [a, b] 区间,因此 M 是未知的。所以,你只能中序遍历树,找出所有落在区间的元素,因此就是 O(N) 的了。
我有一个错误,就是自动把[a,b]想象成整形了,如果不知道的话,还真是O(N)